Verkettung von Blöcken
Im letzten Kapitel wurde der Geheimtext zur Ver- bzw. Entschlüsselung in Blöcke aufgeteilt, die exakt so lang sind wie der Schlüssel. Die Blöcke werden anschliessend einzeln durch die XOR-Funktion mit dem Schlüssel ver- bzw. entschlüsselt.
Prinzipiell kann anstelle der XOR-Funktion jede beliebige mathematische Funktion (resp. Verkettung von Funktionen) zur Verschlüsselung verwendet werden (in den unten aufgeführten Grafiken daher mit dem allgemeinen Begriff block cipher encryption bezeichnet). Wir beschränken uns hier allerdings auf die einfache und gut verständliche XOR-Verschlüsselung.
Der Betriebsmodus «Electronic Code Book» (ECB)
Falls jeder Block mit dem immer gleichen Schlüssel verschlüsselt wird, spricht man vom «Electronic Code Book» (ECB) Betriebsmodus. Schematisch dargestellt sieht dieser wie folgt aus:
 @
@
In der Abbildung wird deutlich, dass ECB kein eigenes Verschlüsselungsverfahren ist, sondern nur ein Modus ist. Er definiert, wie die einzelnen Blöcke verwendet werden. Die konkrete Verschlüsselungsfunktion ist in dieser Darstellung nicht genauer angegeben – wir verwenden der Einfachheit halber hier die XOR-Funktion.
Die Entschlüsselung funktioniert analog: Der Geheimtext wird wiederum in Blöcke aufgeteilt, welche separat mit dem Schlüssel entschlüsselt werden. Die dabei entstandenen Klartext-Blöcke ergeben aneinander gereiht den gesamten Klartext.
 @
@
Der Betriebsmodus «Cipher Block Chaining» (CBC)
Im CBC-Modus werden die Blöcke nicht mehr getrennt voneinander verarbeitet. Wie in der folgenden Abbildung ersichtlich ist, dient jeder Geheimtext-Block (ausser der letzte) im nachfolgenden Schritt zusätzlich als Input. So werden gleiche Klartext-Blöcke trotz identischem Schlüssel zu unterschiedlichen Geheimtextblöcken verschlüsselt.
Das Plus-Zeichen ich Kreis steht hier ebenfalls für die XOR-Operation. Diese ist gegeben, während die Verschlüsselung im grossen Rechteck mit der Bezeichnung block cipher encryption frei gewählt werden kann (also bspw. auch ein aktuell sicheres Verfahren). Da wir in unseren Beispielen allerdings jeweils die XOR-Verschlüsselung als block cipher encryption verwenden, wird bei uns sowohl für die Verrechnung des Klartextblocks mit dem vorherigen Geheimtextblock, wie auch für die eigentliche Verschlüsselung die XOR-Operation verwendet.
Da bei der Verarbeitung des ersten Blocks noch kein Geheimtext-Block zur Verfügung steht, wird als eine Art Platzhalter ein sogenannter Initialisierungsvektor (IV) verwendet.
 @
@
Ändert man 1 Bit im IV, führt dies zu Änderungen im gesamten Geheimtext. Ändert man 1 Bit im Klartext, so ändern sich auch sämtliche darauffolgenden Blöcke im Geheimtext.
Ein Nachteil des CBC-Modus ist allerdings, dass die Verschlüsselung der verschiedenen Blöcke nicht gleichzeitig (also parallel) berechnet werden können, da das Resultat des vorherigen Blocks für die Verschlüsselung des aktuellen Blocks benötigt wird. D.h. ein bestimmter Klartext-Block kann erst verschlüsselt werden, wenn sämtliche vorherigen Blöcke bereits verschlüsselt sind.
Bei der Entschlüsselung sieht es anders aus. Da sofort sämtliche Geheimtextblöcke vorliegen, kann die Entschlüsselung problemlos parallelisiert werden, wie Sie in der folgenden Abbildung nachvollziehen können:
 @
@
Selbstverständlich ist XOR als Verschlüsselungsfunktion aus kryptologischer Sicht nicht ideal – dafür aber für uns gut verständlich, überschaubar und einfach anzuwenden.
In der Realität ist es besonders wichtig, dass die Verschlüsselungsfunktion sämtliche Bits des aktuellen Blocks stark «vermischt». Damit ist gemeint, dass eine winzige Änderung an einer bestimmten Stelle im Klartextblock nicht nur zu einer kleinen Änderung an derselben Stelle im Geheimtextblock führt (wie dies bei XOR wegen der bitweisen Verarbeitung der Fall), sondern dass durch die kleine Änderung viele Bits überall im Block verändert werden.
Aus diesem Grund arbeiten aktuelle Verschlüsselungsfunktionen von Blockchiffren in mehreren Runden.
Rechenbeispiel
In diesem Rechenbeispiel sehen Sie den ECB- und den CBC-Modus im Vergleich.
- Klartext
RAMIRA- Schlüssel
AB- Initialvektor (für CBC)
XY
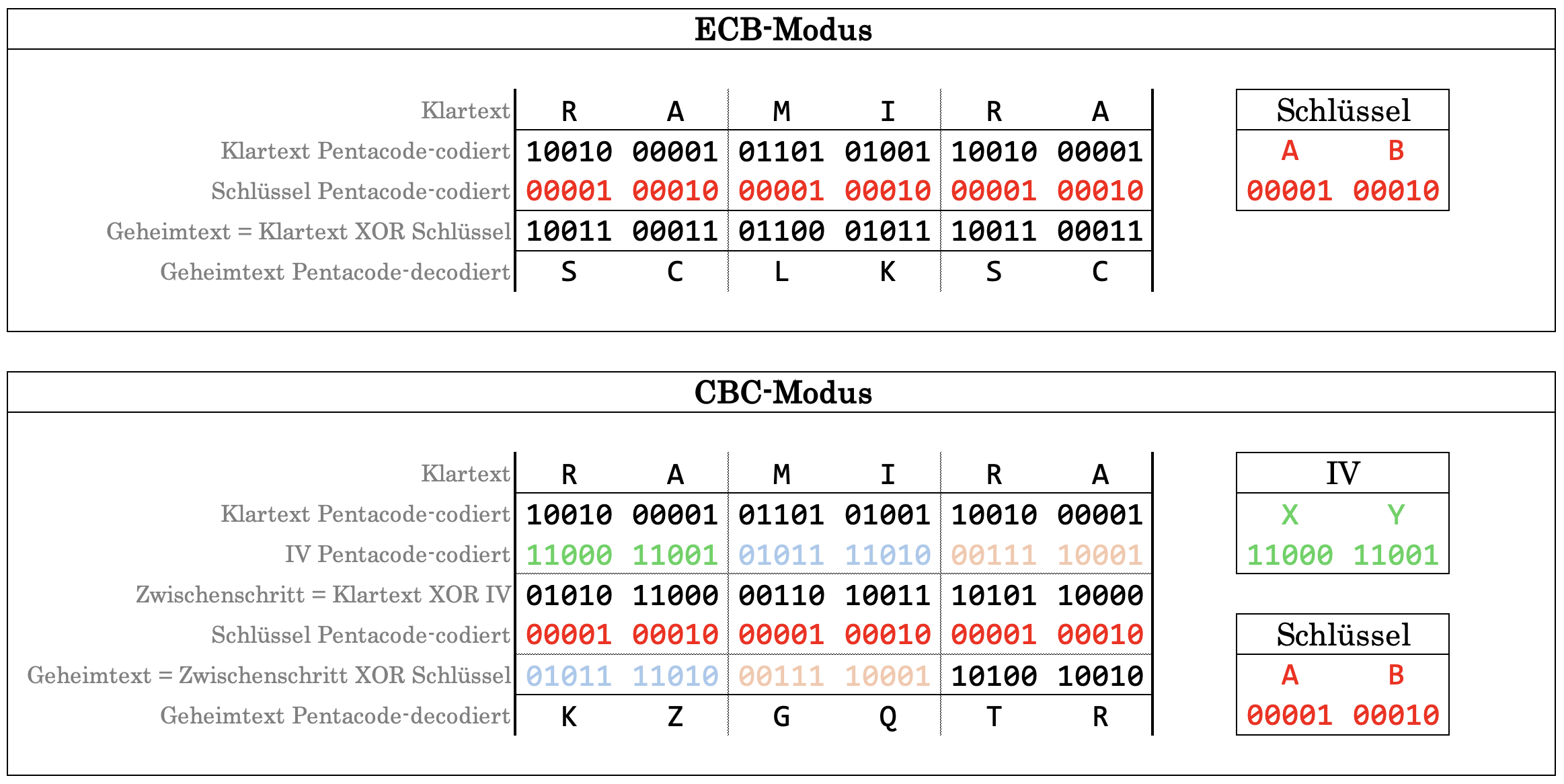
Dieses Beispiel zeigt, was die Verkettung von Blöcken ausmachen kann. Bei beiden Modu werden zwei identische Klartextblöcke RA mit dem Schlüssel AB verschlüsselt.
Beim ECB-Modus weist dementsprechend auch der Geheimtext zwei identische Blöcke SC auf. Durch das Verketten der Blöcke kann diese unschöne Regelmässigkeit mit dem CBC-Modus vermieden werden.
XOR-Blockchiffre ausprobieren
XOR Blockchiffre
Modus
Klartext
Geheimtext
Übungen
ECB-Modus
Lösen Sie diese Übungen von Hand! Sie dürfen einzig den 👉 Pentacode Text-Editor als Hilfsmittel verwenden.
Verschlüsseln Sie den folgenden Text mit der XOR-Blockchiffre im ECB-Modus.
- Text
PAKET ZUGESTELLT- Schlüssel
BETA
- Codieren Sie zuerst den Text mit Pentacode (Sie dürfen dazu den Pentacode Text-Editor verwenden).
- Codieren Sie den Schlüssel ebenfalls mit Pentacode.
- Verschlüsseln Sie den binär dargestellten Text anschliessend mit dem binär dargestellten Schlüssel mittels XOR-Blockchiffre.
- Decodieren Sie die Pentacode-codierte Geheimtext-Bitfolge zu einer Zeichenfolge.
Geben Sie das Resultat hier ein und überprüfen Sie es:
Verschlüsseln Sie den Text BUCHSTABENSPIELE mit dem Schlüssel AKRONYM. Wie lautet der Geheimtext?
Entschlüssen Sie den Geheimtext XWVJZWEKK,XWVJIK mit dem Schlüssel VVXKZ. Wie lautet der Klartext?
CBC-Modus
Lösen Sie diese Übungen von Hand! Sie dürfen einzig den 👉 Pentacode Text-Editor als Hilfsmittel verwenden.
Verschlüsseln Sie den Text WINTER mit dem Schlüssel NY und dem IV AZ. Wie lautet der Pentacode-Geheimtext?
Entschlüsseln Sie den Text NNHDFBA mit dem Schlüssel BE und beliebigem IV.
Geben Sie Ihre Lösung hier ein und kontrollieren Sie anschliessend mit der Musterlösung.
Vertiefungsaufgaben
Verschlüsseln Sie den Klartext BORABORA mit dem Schlüssel RABE. Verwenden Sie dazu die 👉 XOR-Blockchiffre, und zwar zuerst im ECB-Modus und dann im CBC-Modus. Verwenden Sie beim CBC-Modus der Vergleichbarkeit halber den Initialvektor ABCD.
Beantworten Sie anschliessend der Reihe nach die unten stehenden Fragen. Notieren Sie zuerst Ihre Antwort und klappen Sie anschliessend die Frage auf, um den Lösungsvorschlag anzusehen.
Frage 1: Hier passieren einige interessante Dinge. Was fällt Ihnen auf?
Beobachtung 1: Im ECB-Modus erhalten wir den Geheimtext PNPDPNPD - also zweimal hintereinander die Buchstabenfolge PNPD. Auch im Klartext BORABORA finden wir zweimal hintereinander die Buchstabenfolge BORA. Im CBC-Modus sehen wir diese Symmetrie nicht mehr.
Beobachtung 2: Dafür taucht beim CBC-Modus im zweiten Block plötzlich der Initialvektor wieder auf - und zwar egal, mit welchen Initialvektor wir es versuchen.
Frage 2: Wie erklären Sie sich die Beobachtung 1 aus der Antwort zur ersten Frage?
Im ECB-Modus wird jeder Block mit den gleichen Schlüssel verschlüsselt. Wenn also zwei Klartextblöcke identisch sind, dann werden auch die resultierenden Geheimtextblöcke identisch sein. Da der Schlüssel RABE genau halb so lang ist wie der Klartext BORABORA verschlüsseln wir also zweimal den Klartextblock BORA mit dem Schlüssel RABE und erhalten somit zweimal den Geheimtextblock PNPD.
Beim CBC-Modus sehen wir dieses Verhalten nicht mehr, weil wir dort für jeden Block den Output des vorangehenden Blocks als zusätzlichen Input verwenden. Tatsächlich ist dies genau die Idee hinter diesem Verknüpfen von Blöcken.
⭐️ Frage 3: Wie erklären Sie sich die Beobachtung 2 aus der Antwort zur ersten Frage?
Für diese Erklärung verwenden wir für die XOR-Operation das mathematische Symbol . Der Leserlichkeit halber verzichten wir zudem darauf, den Text jeweils explizit ins Binärformat umzuwandeln. Tatsächlich ist die XOR-Funktion aber natürlich nicht für Buchstaben, sonder nur für Binärzahlen definiert!
Mithilfe der 👉 Wahrheitstabelle für die XOR-Verschlüsselung können Sie sich leicht davon überzeugen, dass folgende Gesetze gelten:
Wenn wir nun das Resultat für den ersten Block berechnen wollen, so nehmen wir zuerst den Klartextblock BORA und den Initialvektor ABCD und rechnen . Diesen Input verschlüsseln wir mit der XOR-Verschlüsselung mit dem Schlüsse RABE und erhalten somit insgesamt
Für den zweiten Block verwenden wir diesen Output des ersten Blocks nun aber auch wieder als Input. Auch hier ist der Klartextblock wieder BORA und der Schlüssel wieder RABE. Also erhalten wir für den zweiten Block folgenden Geheimtext:
Wenn wir die Klammern entfernen (die dienen lediglich der Übersicht), so erhalten wir folgende Berechnung:
Weil aber gilt, können wir diese Berechnung wie folgt kürzen:
Und weil wir wissen, dass gilt, so ergibt sich:
Dieses Phänomen tritt also nur deshalb auf, weil wir als Verschlüsselungsmechanismus die XOR-Verschlüsselung verwenden, die "zufällig" auch für die Verkettung verwendet wird. Bei echten Anwendungen von CBC verwenden wir andere, sicherere Verschlüsselungsmechanismen und werden diese Regelmässigkeit deshalb dort nicht antreffen.
Auf den ersten Blick erstaunlich ist die Tatsache, dass die Entschlüsselung mit falschem Initialvektor (IV) nur dazu führt, dass der erste Klartext-Block unleserlich ist, während die restlichen Blöcke korrekt entschlüsselt werden. Weshalb ist das so?
Notieren Sie zuerst Ihre Antwort und vergleichen Sie anschliessend mit der Musterlösung.