Binär

Was mit der Basis $10$ funktioniert, funktioniert auch mit der Basis $2$. Diesmal schauen wir uns die Zahl $101$ an, interpretieren sie aber binär, also zur Basis $2$.

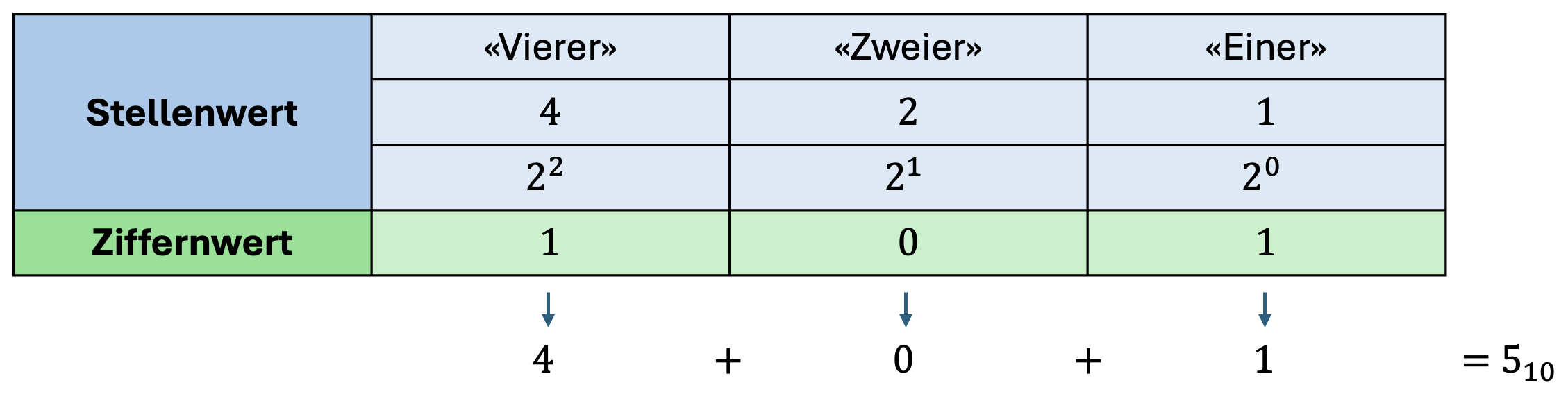
Diese Zahl repräsentiert dann also nicht den Wert "einhunderteins" (in unserem Dezimalsystem), sondern

$1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0 = 1 \cdot 4 + 0 \cdot 2 + 1 \cdot 1$

was dem Wert "fünf" entspricht.

Damit wir wissen, zu welcher Basis wir eine Zahl interpretieren sollen, schreiben wir diese Basis als Index hinter die Zahl: $101_2$. Und somit können wir sagen:

$101_2 = 5_{10}$

Von binär zu dezimal

Die Umrechnung von binär zu dezimal haben wir damit bereits beschrieben: Wir lesen von rechts nach links, wobei die Zahl ganz rechts dem Stellenwert $2^0 = 1$ entspricht, die nächste dem Stellenwert $2^1 = 2$, die übernächste dem Stellenwert $2^2 = 4$, und so weiter. Wenn bei der Stelle eine $1$ steht, addieren wir den Stellenwert zum Zwischenergebnis, wenn eine $0$ steht, lassen wir ihn weg.

2 zu 10

Erledigen Sie die folgenden Umrechnungen ohne Hilfsmittel. Prüfen Sie jeweils Ihre Eingaben.

Binär	Dezimal
$1001$
$10010$
$1011$
$10000001$
$10100000$
$1000110$

Von dezimal zu binär

Für die Umrechnung von dezimal zu binär gibt es zwei Möglichkeiten.

Möglichkeit 1: Division mit Rest

Wir teilen die Dezimalzahl durch die Basis $2$ und merken uns den Rest. Diesen Rest schreiben wir auf, und teilen das Ergebnis erneut durch $2$. Diesen Rest schreiben wir wieder auf, und so weiter, bis das Ergebnis $0$ ist. Die Reste lesen wir dann von unten nach oben, und erhalten so die Binärdarstellung der Zahl.

Möglichkeit 2: Subtraktion

1. Suche die grösste Zweierpotenz, die in der Dezimalzahl Platz hat. Schreibe eine $1$1 und ziehe den Wert der Zweierpotenz von der Dezimalzahl ab.
2. Gehe zur nächstkleineren Zweierpotenz.
3. Prüfe: Hat diese Zweierpotenz in der Dezimalzahl Platz?
   • Ja: Schreibe eine $1$ und und ziehe ihren Wert von der Dezimalzahl ab.
   • Nein: Schreibe eine $0$.
4. Wiederhole ab Schritt 2, bis die kleinste Zweierpotenz erreicht ist.

Am Beispiel $53_{10}$:

Dezimalzahl	Überlegung	Binärzahl
$53$	nächstkleinere Zweierpotenz ist $32$	$1$
$53 - 32 = 21$	$16$ passt in $21$	$1$
$21 - 16 = 5$	$8$ passt nicht in $5$	$0$
$5$	$4$ passt in $5$	$1$
$5 - 4 = 1$	$2$ passt nicht in $1$	$0$
$1$	$1$ passt in $1$	$1$

Binärzal von oben nach unten gelesen: $110101_2$ = $53_{10}$.

Übungen

10 zu 2: Üben

Auf 👉 dieser Seite können Sie das Umrechnen vom Dezimal- zum Binärsystem üben. Üben Sie so lange, bis Sie sich darin sicher fühlen.

10 zu 2: Check

Erledigen Sie die folgenden Umrechnungen ohne Hilfsmittel. Prüfen Sie jeweils Ihre Eingaben.

Eingabeformat

Die Webseite akzeptiert nur Eingaben im Format $1101010$, also ohne Leerzeichen, Hochstriche, etc., und immer mit einer $1$ an erster Stelle.

Dezimal	Binär
$15$
$19$
$96$
$131$
$72$
$128$

---