Huffman-Codierung

David Huffman hat 1952 ein Verfahren entwickelt, mit welchem Zeichen platzsparender codiert werden können. Seine Idee ist, dass Zeichen, welche häufig im Text vorkommen, einen kürzeren Code erhalten, als Zeichen, welche selten im Text vorkommen. Damit unterscheidet sich das Verfahren z.B. von der ASCII-Codierung, bei der alle Zeichen gleich viel Speicherplatz brauchen.

Alltagsbezug

Die Huffman-Codierung und ähnliche Verfahren werden für das Komprimieren von Dateiformaten wie DOCX, JPG oder MP3 eingesetzt.¹

Binärbaum

Ein Binärbaum ist eine Struktur mit genau einem Startknoten, mindestens einem Blattknoten und beliebig vielen Zwischenknoten.

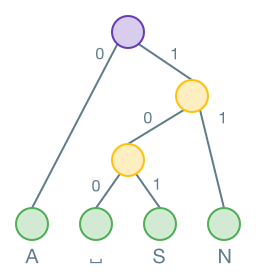
Hier handelt es sich um einen ganz bestimmten Binärbaum: nämlich um einen Huffman-Binärbaum.

Um eine binäre Ziffernfolge mit diesem Baum zu decodieren, startet man beim Startknoten. Von diesem aus geht es entweder nach links oder rechts unten weiter: Steht in der binären Ziffernfolge eine $0$, geht man nach links, bei einer $1$ geht man nach rechts. Wenn man einen Blattknoten (also einen Knoten mit einem Buchstaben) erreicht hat, hat man ein Zeichen decodiert und startet für das nächste Zeichen wieder beim Startknoten.

Nehmen wir als Beispiel die folgenden Daten:

0111101011000110110101

Die erste $0$ führt uns vom Startknoten direkt zum Buchstaben A.

0|111101011000110110101 → A

Anschliessend folgt eine $1$. Wir starten wieder beim Startknoten und kommen zum oberen Zwischeknoten. Es folgt nochmal eine $1$, womit wir beim Buchstaben N landen.

011|1101011000110110101 → AN

Beispiel fertigstellen

Fahren Sie nach demselben Prinzip weiter, bis Sie die gesamte binäre Zeichenfolge abgearbeitet und so den Text decodiert haben.

Geben Sie den decodierten Text hier ein (alles in Grossbuchstaben) und überprüfen Sie Ihre Antwort.

Erstellen eines Huffman-Baums

Der obige Huffman-Binärbaum ist natürlich nicht allgemeingültig. Für jeden Text, den wir komprimieren wollen, erstellen wir einen individuellen Huffman-Baum. Die damit codierten Daten lassen sich demnach auch nur mit genau diesem Baum wieder decodieren.

Wie der Huffman-Algorithmus funktioniert, soll am Beispiel der Codierung des Texts EINTRITT FREI gezeigt werden.

Zuerst zählt man, wie oft jedes Zeichen im Text vorkommt und erstellt eine Häufigkeitstabelle.

Zeichen	Häufigkeit
E	2
I	3
N	1
T	3
R	2
␣	1
F	1

Nun geht es darum, einen Binärbaum zu erstellen. Dazu wird zunächst für jeden Buchstaben ein Knoten gebildet. Die Häufigkeit steht im Knoten, der Buchstaben darunter:

Nun werden die zwei Knoten mit den kleinsten Häufigkeiten an einen neuen Knoten angehängt. Der neue Knoten enthält die Summe der Häufigkeiten der ursprünglichen Knoten:

Dies wird wiederholt, bis alle Knoten miteinander verbunden sind. Wenn zwei Knoten die gleiche Häufigkeit haben, spielt es keine Rolle, welcher gewählt wird. Im nächsten Schritt wird der kleinste Knoten N mit R zusammengefasst. Es könnten aber auch N und E oder N und der neu erstellte Knoten zusammengefasst werden. Die Lösung ist somit nicht eindeutig: Es gibt mehrere korrekte Lösungen!

Wichtig ist, dass immer die kleinsten Knoten zusammengefasst werden. Hier werden die zwei Knoten mit Häufigkeit $2$ zusammengefasst:

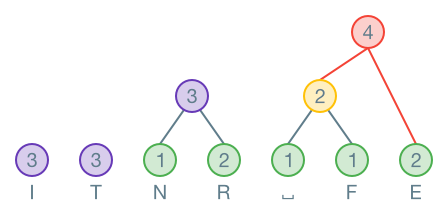
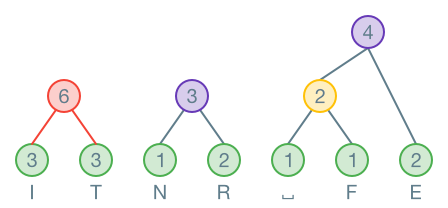
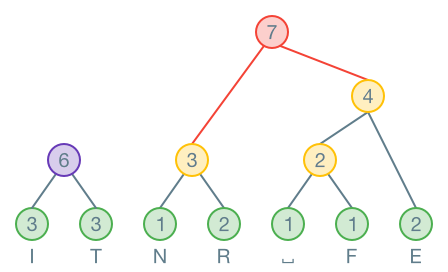
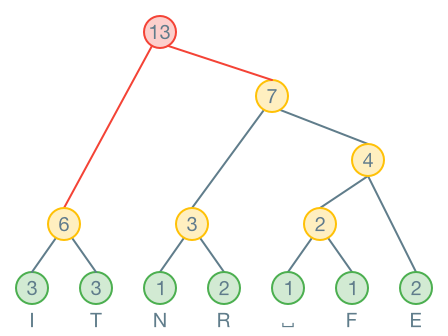
Wenn der Baum fertig ist, werden alle Äste, welche nach links zeigen, mit einer $0$ markiert. Alle die nach rechts zeigen, werden mit einer $1$ markiert.

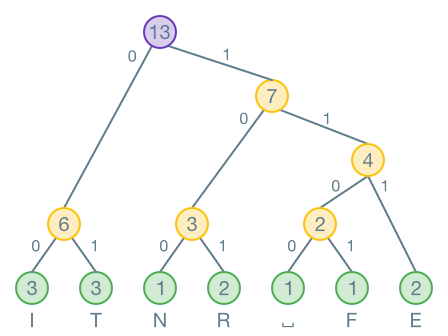
Nun kann eine Codierungstabelle erstellt werden, indem der Code für jedes Zeichen vom Baum abgelesen wird:

Zeichen	Code
I	00
T	01
N	100
R	101
E	111
⎵	1100
F	1101

Mit dieser Codierungstabelle können wir nun – genau wie z.B. mit der ASCII-Tabelle – den Text binär codieren.

Das Resultat: EINTRITT FREI → 11100100011010001011100110110111100.

Elemente einer Huffman-Codierung

Eine abgeschlossene Huffman-Codierung besteht also aus folgenden Elementen:

• Häufigkeitstabelle
• Huffman-Baum
• Codierungstabelle
• Huffman-codierter Text (Binärdaten)

Kompressionsverhältnis

Wie effizient wurde hier komprimiert?

Zählen Sie zuerst die Anzahl Bits in den Huffman-codierten Binärdaten. Überlegen Sie anschliessend, wie viele Bits wir für den Text EINTRITT FREI benötigen, wenn wir ihn ganz normal mit 8-Bit ASCII codieren.

Rechnen Sie anschliessend

$C = 100 \cdot (1 - \frac{\text{Anz. Bits mit Huffman}}{\text{Anz. Bits mit ASCII}})$

um das Kompressionsverhältnis $C$ dieser Huffman-Codierung in $\%$ des ASCII-codierten Vergleichswerts zu erhalten.

Geben Sie das Resultat hier ein (inkl. $\%$-Zeichen, gerundet auf eine Ganzzahl):

Kompressionsverhältnis

So viel $\%$ an Speicherplatz sparen wir also ein, wenn wir den Text mit Huffman statt mit 8-Bit ASCII codieren.

Übungen

Texte codieren

Gegeben sind folgende Texte:

1. MISSISSIPPI
2. EXTERNER EFFEKT

Gehen Sie für beide Texte einzeln je so vor:

1. Erstellen Sie eine Häufigkeitstabelle.
2. Erstellen Sie den Huffman-Baum.
3. Erstellen Sie daraus die Codierungstabelle.
4. Codieren Sie den Text mit der Codierungstabelle.

Bearbeiten Sie die beiden Texte als zwei separate Teilaufgaben. Arbeiten Sie auf Papier. Vergleichen Sie Ihre Resultate am Schluss mit der Musterlösung.

Laden...

Verlustfrei oder verlustbehaftet?

Handelt es sich bei Huffman um eine verlustfreie oder eine verlustbehaftete Kompression? Begründen Sie.

Laden...

Laden...

⭐️ Exkurs: Bezug zu UTF-8

«Im Gegensatz zu ASCII ist UTF-8 ebenfalls eine Form der Kompression, weil dabei nicht jedes Zeichen gleich viele Bytes braucht.»

Diskutieren Sie diese These. Stimmen Sie Ihr zu? Wieso (nicht)?

Laden...

Laden...

Footnotes

1. Wikipedia: 👉 Huffman coding. ↩